Classification & Clustering 의 성능 평가 지표
Linear모델에 대해서는 MSE, R-square 등으로 모델의 성능을 평가할 수 있다. 그렇다면 분류 모델 또는 클러스터링에서의 성능 평가 방법은 어떠할까? 사실 분류 모델과 클러스터링은 평가 방법이 다르다. 이 둘의 차이는 라벨(정답)의 유무인데, 클러스터링은 라벨이 없는 상태에서 클러스터의 응집도 등으로 평가를 진행한다. 하지만 이또한 정확도가 높지 않기 때문에 전문 지식을 가지고 있는 도메인 전문가의 휴리스틱한 평가 방식을 취한다.
Classification의 성능 평가 지표 - Confusion Matrix

이진 분류(양성, 음성)을 다루는 task라고 했을 때 모델의 정확도가 100%이면 아래와 같이 양성으로 예측된 영역을 Positive prediction, 음성으로 예측된 영역을 Negative prediction으로 정의한다.

이렇게 100%의 정확도로 예측하는 모델이 있으면 좋으렸만, 현실에서는 그러기가 힘들다
현실세계에서의 모델 예측은 아래와 같다.

- 양성인데, 양성으로 제대로 검출된것은 True Positive (TP)
- 음성인데 음성으로 제대로 검출된것은 True Negative (TN)
- 양성인데 음성으로 잘못 검출된것은 False Negative (FN)
- 음성인데 양성으로 잘못 검출된것은 False Positive (FP)
그래서 우리에게 자주 등장하는 표는 아래와 같다.

Accuracy (정확도)
모델이 바르게 분류한 부분으 비율로, Confusion Matrix에서 대각선 부분에 해당한다.
$ACC = \frac{TP + TN}{TP + FN + FP + TN}$

Error rate (오류율)
Error Rate는 Accuracy와 반대로, 전체 데이터 중에서 잘못 분류한 비율을 나타냄
$Error rate = \frac {FN + FP}{TP + FN + FP + TN}$
Precision (정밀도)
모델이 Positive라 분류한 것 중에 실제 Positive인 비율
$Precision = \frac {TP} / {TP + FP}$

Precision is about being precise. In common English, being precise means: if you give an answer, the answer will very likely be correct. So even if you answered only one question, and you answered this question correctly, you are 100% precise.
Recall = Sensitivity (True Positive Rate)
실제 값이 Positive인 것 중 모델이 Positive라 분류한 비율 = 모델이 얼마나 정확하게 Positive값을 찾느냐
민감도라고도 하는 recall은 원래 Positive데이터 수 중에서 Positive로 분류된 수를 이야기 한다. 예를 들어 실제 암 양성이 100개이면 모델에서 90개라고 분류하였으면 recall = 0.9
$Recall = \frac {TP} / {TP + FN}$

Recall (as opposed to precision) is not so much about answering questions correctly but more about answering all questions that have answer "true" with the answer "true". So if we simply always answer "true", we have 100% recall.
False Positive Rate (FPR)
원래는 Negative인데, 잘못해서 Positive로 판단한 비율 (positive라고 예측한게 틀린 비율)
$FPR = \frac {FP} / {TN + FP}$
어뷰징에서는 정확도도 중요하지만, 정상 사용자를 비정상 사용자라고 검출하는 경우(FPR)에 대해 패널티를 부여하기 때문에, 아무리 어뷰징 사용자를 잘 찾아낸다 하더라도 FPR갚을 높이게 되면, 정상적인 사용자를 어뷰징 사용자로 판단하여 착한 사용자에게 패널티를 부여하는 일이 생기기 때문에, 문제가 될 수 있다. 어뷰징 사용자를 많이 찾아내는 것보다, 정상 사용자가 징계를 받게 되는 경우 비지니스에 크리 티컬 할 때 FPR값을 참조 할 수 있다.
F1 score
F1 score는 Precision과 Recall의 조화 평균 값이다.
When measuring how well you're doing, it's often useful to have a single number to describe your performance
When measuring how well you're doing, it's often useful to have a single number to describe your performance. We could define that number to be, for instance, the mean of your precision and your recall. This is exactly what the F1-score is.
$F1_score = \frac {w * Precision * Recall} / {Precision + Recall}$

왜 F1 score를 써야 할 까?? - 데이터 불균형 때문에
예를 들어 아래와 같은 경우가 있다고 했을 때 (A class에만 데이터가 편중되어 있다) A-200, B-10, C-10, D-0

- Model 1은 A class에 대해서 예측률은 좀 떨어지지만, B,C,D에 대해서는 전반적으로 잘 맞춤
- Model 2은 오직 A class에 대해서만 잘 맞춤.
- 문제는 accuracy를 구해보면
- Model1 : (100+9+8+9)/230 = 0.547
- Model2 : (198+1+1+1)/230 = 0.87
- 반대로 F1 score를 구해보면
- Model1 : (2*0.492*0.775)/(0.492+0.775) = 0.601
- Model2 : (2*0369*0.323)/(0.369+0.323) = 0.344
data가 불균형하면 Precision대신 F1 스코어를 사용한다.

F 스코어를 구하는 방식
$F_{\beta} = \frac{(1+\beta^{2})(Precision*Recall)}{\beta^{2}*Precision*Recall}$
$\beta가 2일때가 F1 스코어$
ROC (Receiver Operating Characteristics)
ROC 그래프는 가로축을 FR rate (specificity)값의 비율로 하고 세로를 TP rate(sensitive)로 하여 시각화한 그래프.
- Specificity = TN / TN + FP
- Sensitive(Recall) = (TP) / P
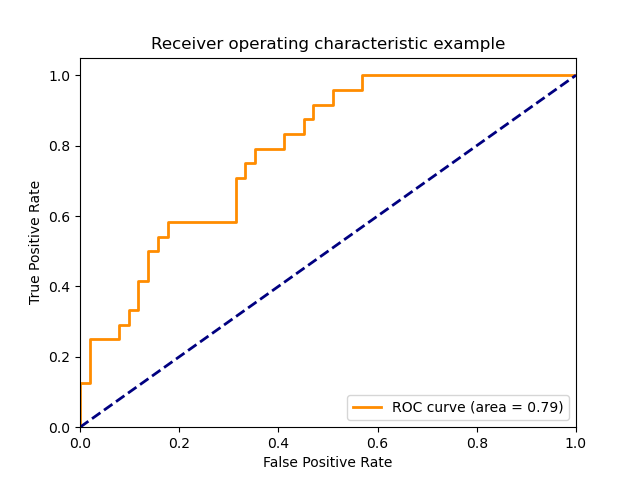
위의 정의를 생각하면, 당연하게도 그래프가 이로 갈 수록 좋은 모델이다. 임계점은 x = y 선으로 두고 이보다 낮게 있으면 쓸 수 있는 모델로 볼 수가 없다.
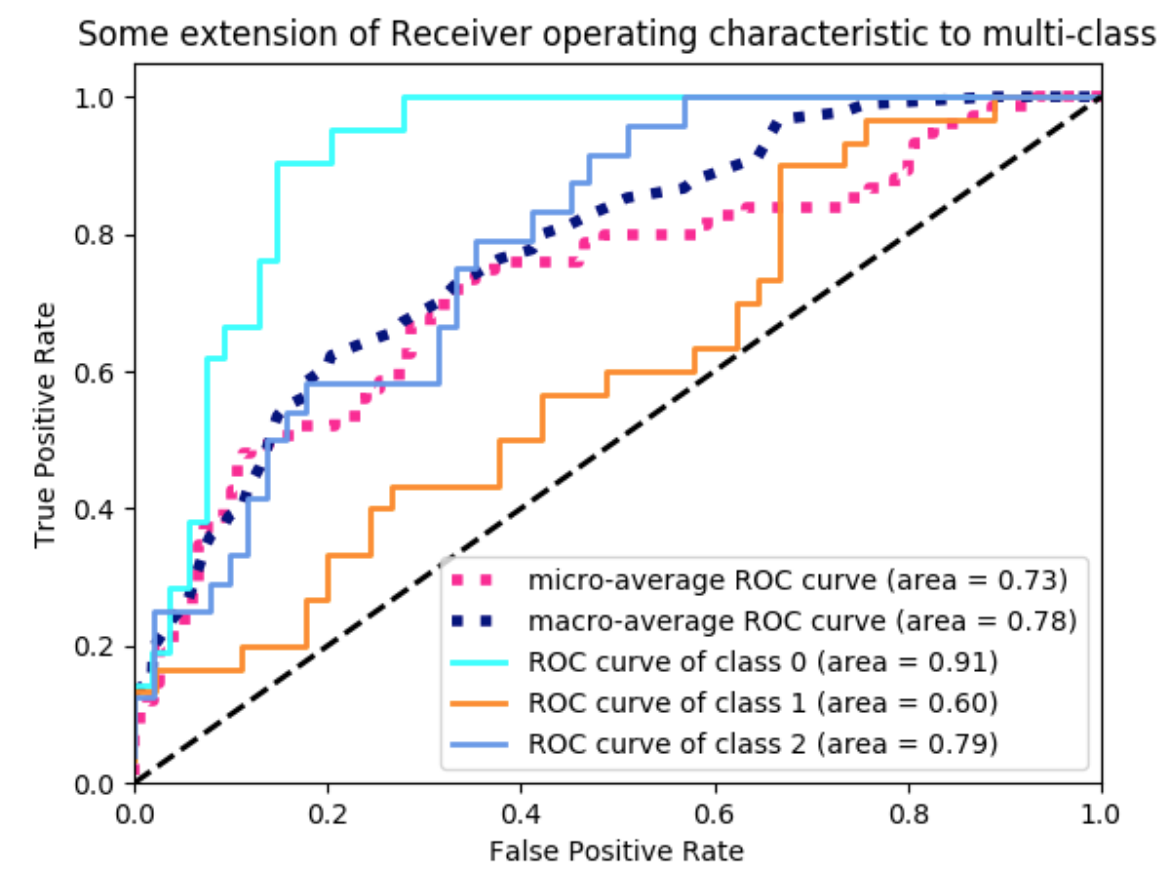
ROC 커브는 각 클래스마다 그릴 수 있는데, 위와 같은 그래프에서 class 0 이 가장 높다. 이 의미는 해당 모델이 class 0을 가장 잘 분류하고 그 다음으로 2,1의 순서로 분류를 잘 한다는 의미이다. 이렇게 명확하게 위에 있다면 어떤 모델이 좋은지 해석하기가 명확할 것이다. 하지만 그래프가 어떤게 위에 찍히는지 명확하게 보이지 않을 경우, 우리는 정확도를 숫자로 나타내기 위해 AUC(Area Under Curve)값을 이용한다. ROC AUC는 다시말해, 그래프의 아래 면적이 되는 것이다.
모델을 평가할 때 지표의 사용
일반적으로 accuracy가 많이 사용되고, 그 외에 ROC, Precision, Recall plot, F-score등이 많이 사용 됨
[reference]
분류모델 (Classification)의 성능 평가
Classification & Clustering 모델 평가 조대협 (http://bcho.tistory.com) 클러스터링과 분류 모델에 대한 성능 평가 방법은 데이타에 라벨이 있는가 없는가에 따라서 방법이 나뉘어 진다. 사실 클러스터링은
bcho.tistory.com
분류 모델 성능 평가 지표 - Confusion Matrix란? :: 정확도(Accuracy), 정밀도(Precision), 재현도(Recall), F1 Sc
분류 모델 성능 평가 지표 Linear 모델에 대해서는 R-Square, MSE 등 으로 모델의 성능을 평가한다. 그렇다면 분류 모델에 대해서는 모델의 성능을 어떻게 평가할 수 있을까? 여러가지 방법이 있지만,
leedakyeong.tistory.com
'Machine Learning' 카테고리의 다른 글
| [Pytorch] 모델 구조 확인, parameter확인 (0) | 2021.11.16 |
|---|---|
| [pytorch] tensor 초기화 및 속성 (0) | 2021.11.15 |
| [Pytorch] model.train(), model.eval() 의미 (0) | 2021.10.27 |
| [cs231n] 내가보려고만든 cs231n 강의자료모음집 (0) | 2021.06.06 |
| [Pytorch] torch.manual_seed() (1) | 2021.03.22 |